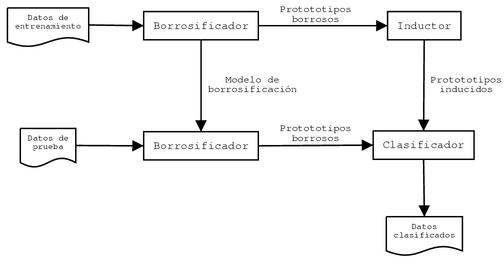
Aprendizaje automático basado en prototipos

En algunos casos, el diseño de modelos matemáticos que describan un cierto problema requiere la representación de conceptos vagos, bien por falta de información o por la vaguedad intrínseca del concepto en sí.

En estos casos, las teorías matemáticas clásicas resultan inadecuadas, ya que están pensadas para representar conceptos nítidos.

Un buen ejemplo de ello es la teoría de conjuntos. En ella, un elemento dado pertenece a un conjunto siempre de forma absoluta: o bien pertenece totalmente, o bien no pertenece en absoluto. No se admite ningún grado intermedio.

La teoría de subconjuntos borrosos extiende la teoría clásica de conjuntos para admitir la representación de conjuntos imprecisos, en los que un elemento no sólo puede pertenecer (o no) totalmente, sino también de forma parcial.

Empleando subconjuntos borrosos pueden representarse realidades genéricas o vagas, y definir reglas lógicas que operan sobre ellas, reproduciendo, en cierta medida, la forma de pensamiento humano que con frecuencia se basa en nociones imprecisas y subjetivas.

El principal objetivo del sistema FLPD es el aprendizaje automático. Por aprendizaje automático se entiende el proceso mediante el cual un sistema (informático) es capaz de extraer información de un conjunto de ejemplos, para después aplicarla de forma autónoma sobre nuevos casos.

La aplicación típica de este tipo de sistemas se da en tareas de clasificación: se quiere discriminar el tipo o clase al que pertenecen una serie de elementos en función de un conjunto limitado de parámetros (atributos) que se conocen de cada uno de ellos.

Para ello se lleva a cabo un proceso de inducción sobre un conjunto base de elementos cuya clase ya se conoce (conjunto de entrenamiento), para obtener un clasificador, capaz de emplear la información sintetizada a partir de los ejemplos dados para clasificar nuevos elementos.

Existen diversas estrategias para extraer y representar información significativa de un conjunto de ejemplos. En el sistema FLPD se emplean prototipos: a partir de los datos de ejemplo se genera un conjunto (reducido) de prototipos que sintetizan la información común a los datos dados.

Un prototipo es, sencillamente, un conjunto de valores asociados a una serie de atributos. En cierto modo, los datos originales también son prototipos. En este sistema, sin embargo, se representan los prototipos de una forma especial, como se describe más abajo.

Una vez inducidos los prototipos, el sistema clasifica nuevos datos comparándolos con los prototipos que ha inferido. El esquema de funcionamiento de una clasificación supervisada sería el siguiente:

Los elementos que constituyen el esquema anterior son:

El sistema FLPD utiliza un algoritmo de inducción denominado HPI (Hierarchical Prototype Induction), que, a partir de los datos originales, genera un conjunto de prototipos obtenidos mediante un proceso de inducción en sucesivos niveles.

Para representar estos prototipos, que han de sintetizar la mayor cantidad posible de información acerca de los datos originales, se emplean prototipos borrosos.

Un prototipo borroso está compuesto por un conjunto de conjuntos borrosos (valga la redundancia) asociados a una serie de atributos. El uso de conjuntos borrosos permite un cierto grado de imprecisión que facilita la representación de información genérica o prototípica.

La utilización de prototipos borrosos requiere, por una parte, la transformación de los datos originales en datos borrosos, y, por otra, la definición de las herramientas matemáticas apropiadas para comparar y combinar prototipos borrosos.